Difference between revisions of "Arquímedes de Siracusa. N15"
(→Bibliografía) |
(→Bibliografía) |
||
| Line 98: | Line 98: | ||
http://es.wikipedia.org/wiki/Arqu%C3%ADmedes | http://es.wikipedia.org/wiki/Arqu%C3%ADmedes | ||
| − | + | http://mimosa.pntic.mec.es/jgomez53/matema/conocer/arquimedes.htm | |
Revision as of 14:02, 26 March 2014
Contents |
Introducción
En este vídeo vamos a ver el Episodio 02 de Erase una vez los Inventores. En este vídeo no solo nos muestran los inventos de Arquímedes, sino también de muchos otros antiguos que descubrieron muchas cosas.
Biografía
Arquímedes de Siracusa nació en Siracusa (Sicilia) en el 287 a. C. y falleció en el 212 a.C. durante el “sitio de Siracusa”. Fue un físico, ingeniero, inventor, astrónomo y matemático griego. Aunque se conocen pocos detalles de su vida, es considerado uno de los científicos más importantes de la antigüedad clásica. Entre sus avances en física se encuentran sus fundamentos en hidrostática, estática y la explicación del principio de la palanca. Es reconocido por haber diseñado innovadoras máquinas, incluyendo armas de asedio y el tornillo de Arquímedes utilizado para elevar agua, la polea compuesta, el torno, la rueda dentada, el principio de la hidrostática y la ley de la palanca. Experimentos modernos han probado las afirmaciones de que Arquímedes llegó a diseñar máquinas de guerra basadas en palancas, catapultas y un sistema de espejos con el que logró incendiar las naves romanas.
Se considera que Arquímedes fue uno de los matemáticos más grandes de la antigüedad y uno de los más importantes de la historia. Usó el método exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número Pi. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy largos. También debemos añadir que fue este ámbito el que más desarrolló ya que ante todo él se consideraba un verdadero geómetra colaborando en el desarrollo que se daría casi 2000 años más tarde del cálculo integral.
A diferencia de sus inventos, los escritos matemáticos de Arquímedes no fueron muy conocidos en la antigüedad. Los matemáticos de Alejandría lo leyeron y lo citaron, pero la primera recopilación integral de su obra no fue realizada hasta el 530 d. C. por Isidoro de Mileto. Los comentarios de las obras de Arquímedes escritos por Eutocio en el siglo VI las abrieron por primera vez a un público más amplio. Las relativamente pocas copias de trabajos escritos de Arquímedes que sobrevivieron a través de la Edad Media fueron una importante fuente de ideas durante el Renacimiento, mientras que el descubrimiento en 1906 de trabajos desconocidos de Arquímedes en el Palimpsesto de Arquímedes ha ayudado a comprender cómo obtuvo sus resultados matemáticos.
Descubrimientos
Uno de sus grandes inventos fue el tornillo de Arquímides que consistía en una máquina que era era un mecanismo con una hoja con forma de tornillo dentro de un cilindro. Se hacía girar por medio de una manivela, y podía utilizarse para transportar agua a niveles mas altos.
Principio de Arquímedes
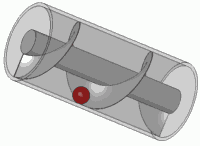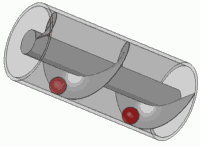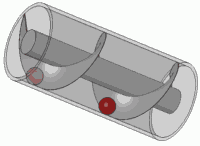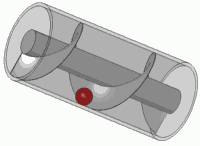
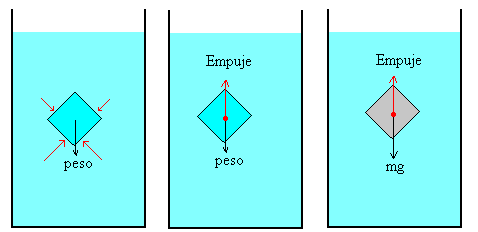
El principio de Arquímedes es un principio físico que afirma que: «Un cuerpo total o parcialmente sumergido en un fluido en reposo, recibe un empuje de abajo hacia arriba igual al peso del volumen del fluido que desaloja». Esta fuerza recibe el nombre de empuje hidrostático o de Arquímedes, y se mide en newtons (en el Sistema Internacional de Unidades). El principio de Arquímedes se formula así:
| fórmula |
|---|
| E = m\;g = \rho_\text{f}\;g\;V\; |
o bien
| fórmula |
|---|
|
\mathbf E = - m\;\mathbf g = - \rho_\text{f}\;\mathbf g\;V\; |
Donde E es el empuje , ρf es la densidad del fluido, V el «volumen de fluido desplazado» por algún cuerpo sumergido parcial o totalmente en el mismo, g la aceleración de la gravedad y m la masa, de este modo, el empuje depende de la densidad del fluido, del volumen del cuerpo y de la gravedad existente en ese lugar. El empuje (en condiciones normales y descrito de modo simplificado ) actúa verticalmente hacia arriba y está aplicado en el centro de gravedad del fluido desalojado por el cuerpo; este punto recibe el nombre de centro de carena.
Principio de Arquímedes de Siracusa
Historia del Principio de Arquímedes
Según se cree, Arquímedes fue llamado por él el rey Herón de Siracusa, donde Arquímedes vivió en el siglo III A.C., para dilucidar el siguiente problema. Se cuenta que el rey Herón de Siracusa le había entregado a un platero una cierta cantidad de oro para con ella le hiciera una corona. Cuando estuvo terminada, se decía que el platero había sustituido una parte del oro por una cantidad equivalente de plata, devaluando con ello la corona y engañando, pues, al rey.
El rey encargó a Arquímedes que descubriera si había sido engañado. El problema que Arquímedes debía resolver era determinar si el joyero había sustraído parte del oro o no, pero no podía romper la corona para averiguarlo. Arquímedes pensó arduamente cómo resolver el problema, sin poder encontrar una solución.
Se dice que mientras se disponía a bañarse en una tina, en la que por error había puesto demasiada agua, al sumergirse en ella, parte del agua se derramó. Arquímedes se dio cuenta de que este hecho podía ayudarle a resolver el enigma planteado por Herón y fue tal su regocijo que, desnudo, salió corriendo de la tina gritando "¡Eureka, eureka!" (que significa "¡Lo encontré, lo encontré!").
http://www.youtube.com/watch?v=a0rXe7EwqKg (no sé si quitar porque el mío es mejor) http://hidrostaticafisica2.blogspot.com.es/p/principio-de-arquimides.html (no sé si quitar porque el mío es mejor)
--Juliaroman (talk) 14:11, 12 March 2014 (MET)
Demostración física
Cualquier cuerpo parcial o totalmente sumergido en un fluido sufre una fuerza vertical hacia arriba, llamada empuje, que es igual al peso del fluido que desaloja.
Imagina un cuerpo, por ejemplo, la corona de Arquímedes. Ahora imagina que el mismo cuerpo, con la forma exacta de la corona metálica estuviera hecho de agua –pues ése era el fluido en el caso de la historia– en vez de hecho de metal. ¿Cuánto pesaría esa “corona de agua”? Ése es el valor de la fuerza hacia arriba –el empuje– que sufre la corona metálica.
Un ejemplo es el de la pelota y la piscina. Estás tranquilamente en el agua, con una pelota junto a ti, e intentas meter la pelota bajo el agua, pero te cuesta muchísimo. ¿Cómo puede ser tan difícil hundir la pelota diez centímetros? Porque, en tu cabeza, estás haciendo una cosa: hundir la pelota. Pero, en la realidad, estás haciendo dos cosas, una muy fácil y otra no tanto: bajar la pelota y subir el agua.
Agradecimientos
Bibliografía
Alfredo Loayza y Tere Ledezma (abril de 2012). Hidrostática: Principio de Arquímedes. Consultado el 12 marzo de 2014. En:http://hidrostaticafisica2.blogspot.com.es/p/principio-de-arquimides.html
Elbesodenarciso.(30-05-2010). Arquimedes - Inventos y Descubrimientos. Taringa! inteligencia colectiva. Consultado el 12 del III del 2014. http://www.taringa.net/posts/ciencia-educacion/5645290/Arquimedes---Inventos-y-Descubrimientos.html
Principio de Arquímedes de Siracusa http://hidrostaticafisica2.blogspot.com.es/p/principio-de-arquimides.html
Arquímedes.(2014,marzo 3).Wikipedia: La enciclopedia libre. Consultado el 12 de marzo de 2014. En: http://es.wikipedia.org/wiki/Arquímedes es.wikipedia.org/wiki/Arquímedes.
http://www.biografiasyvidas.com/biografia/a/arquimedes.htm
http://es.wikipedia.org/wiki/Arqu%C3%ADmedes
http://mimosa.pntic.mec.es/jgomez53/matema/conocer/arquimedes.htm