Difference between revisions of "Arquímedes de Siracusa. N15"
(→Biografía) |
MariaJesus (Talk | contribs) |
||
| (74 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
== Introducción == | == Introducción == | ||
| − | |||
| − | |||
| − | |||
| − | + | En este vídeo vamos a ver el Episodio 02 | |
| + | de Erase una vez los Inventores. En este | ||
| + | vídeo no solo nos muestran los inventos | ||
| + | de Arquímedes, sino también de muchos | ||
| + | otros antiguos que descubrieron muchas | ||
| + | cosas. | ||
| − | + | {{#ev:youtube|2SCfgi-pYsA}} | |
| − | + | En este trabajo os vamos a hablar sobre Arquímedes de Siracusa y sus grandes teorías, y para ello, tenemos una breve introducción antes de adentrarnos en su biografía. | |
| − | + | Arquímedes fue un físico, ingeniero, inventor, astrónomo y matemático griego. Aunque se conocen pocos detalles de su vida, es considerado uno de los científicos más importantes de la antigüedad clásica. Entre sus avances en física se encuentran sus fundamentos en hidrostática, estática y la explicación del principio de la palanca. Es reconocido por haber diseñado innovadoras máquinas, incluyendo armas de asedio y el tornillo de Arquímedes utilizado para elevar agua, la polea compuesta, el torno y la rueda dentada. Experimentos modernos han probado las afirmaciones de que Arquímedes llegó a diseñar máquinas de guerra basadas en palancas, catapultas y un sistema de espejos con el que logró incendiar las naves romanas. | |
| − | + | ||
| + | Se considera que Arquímedes fue uno de los matemáticos más grandes de la antigüedad y uno de los más importantes de la historia. Usó el método exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número Pi. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy largos. También debemos añadir que fue este ámbito el que más desarrolló ya que ante todo él se consideraba un verdadero geómetra colaborando en el desarrollo que se daría casi 2000 años más tarde del cálculo integral. | ||
| + | |||
| + | Las relativamente pocas copias de trabajos escritos de Arquímedes que sobrevivieron a través de la Edad Media fueron una importante fuente de ideas durante el Renacimiento, mientras que el descubrimiento en 1906 de trabajos desconocidos de Arquímedes en el Palimpsesto de Arquímedes ha ayudado a comprender cómo obtuvo sus resultados matemáticos. | ||
== Biografía == | == Biografía == | ||
| − | [[File:Arquimedes.jpg | + | [[File:Arquimedes.jpg|200px|thumbnail|right|Arquimedes]] |
| − | + | ||
| − | + | Nació en Siracusa en el 287 a.C y murió en el 212 a.C. Matemático griego. Hijo de un astrónomo, Arquímedes estudió en Alejandría, donde tuvo como maestro a Conón de Samos y entró en contacto con Eratóstenes. Regresó luego a Siracusa, donde se dedicó al trabajo científico. | |
| − | + | ||
| + | Arquímedes: | ||
| + | Gran matemático e ingeniero, a quien Plutarco atribuyó una «inteligencia sobrehumana. La más divulgada la relata Vitruvio y se refiere al método que utilizó para comprobar si existió fraude en la confección de una corona de oro encargada por Hierón II, tirano de Siracusa y protector de Arquímedes. Hallándose en un establecimiento de baños, advirtió que el agua desbordaba de la bañera a medida que se iba introduciendo en ella; esta observación le inspiró la idea que le permitió resolver la cuestión que le planteó el tirano. Se cuenta que, impulsado por la alegría, corrió desnudo por las calles de Siracusa hacia su casa gritando «Eureka! Eureka!». | ||
| + | |||
| + | La idea de Arquímedes está reflejada en su obra Sobre los cuerpos flotantes, corresponde al famoso principio que lleva su nombre y, como allí se explica, haciendo uso de él es posible calcular la ley de una aleación, lo cual le permitió descubrir que el orfebre había cometido fraude. | ||
| + | |||
| + | Otra anécdota famosa, recogida por Plutarco, entre otros, Arquímedes aseguró al tirano que," si le daban un punto de apoyo, conseguiría mover la Tierra"; se cree que, exhortado por el rey a que pusiera en práctica su aseveración, logró sin esfuerzo, mediante un complicado sistema de poleas, poner en movimiento un navío de tres mástiles con su carga. | ||
| + | |||
| + | Son célebres los ingenios bélicos, que permitieron a Siracusa resistir tres años el asedio romano, antes de caer en manos de las tropas de Marcelo; también se cuenta que, contraviniendo órdenes expresas del general romano, un soldado mató a Arquímedes por resistirse a abandonar la resolución de un problema matemático en el que estaba trabajando. | ||
| + | |||
| + | La pasión de Arquímedes por el conocimiento , que le causó la muerte, fue también la que, en vida, soliera entretenerse trazando dibujos geométricos en las cenizas del hogar o incluso, al ungirse, en los aceites que cubrían su piel. Esta imagen contrasta con la del inventor de máquinas de guerra del que hablan Polibio y Tito Livio; pero, como señala Plutarco, su interés por esa maquinaria estribó únicamente en el hecho de que planteó su diseño como mero entretenimiento intelectual. | ||
| + | |||
| + | El esfuerzo de Arquímedes por convertir la estática en un cuerpo doctrinal riguroso es comparable al realizado por Euclides con el mismo propósito respecto a la geometría; esfuerzo que se refleja de modo especial en dos de sus libros: en los Equilibrios planos fundamentó la ley de la palanca, deduciéndola a partir de un número reducido de postulados, y determinó el centro de gravedad de paralelogramos, triángulos, trapecios, y el de un segmento de parábola. En la obra Sobre la esfera y el cilindro utilizó el método denominado de exhaustión, precedente del cálculo integral, para determinar la superficie de una esfera y para establecer la relación entre una esfera y el cilindro circunscrito en ella. Este último resultado pasó por ser su teorema favorito, que por expreso deseo suyo se grabó sobre su tumba, hecho gracias al cual Cicerón pudo recuperar la figura de Arquímedes cuando ésta había sido ya olvidada. | ||
== Descubrimientos == | == Descubrimientos == | ||
| − | + | ||
Uno de sus grandes inventos fue el tornillo de Arquímides que consistía en una máquina que era era un mecanismo con una hoja con forma de tornillo dentro de un cilindro. Se hacía girar por medio de una manivela, y podía utilizarse para transportar agua a niveles mas altos. | Uno de sus grandes inventos fue el tornillo de Arquímides que consistía en una máquina que era era un mecanismo con una hoja con forma de tornillo dentro de un cilindro. Se hacía girar por medio de una manivela, y podía utilizarse para transportar agua a niveles mas altos. | ||
| − | [[File:Tornillo de Arquímedes.gif|left]] | + | |
| − | + | [[File:Tornillo de Arquímedes.gif|left]] Otro de sus inventos fue la garra de Arquímedes. Es un arma que fue hecha para defender la ciudad de Siracusa del ataque romanos. También conocida como "el agitador de barcos", la garra consistía en un brazo parecido a una grúa con un gran gancho de metal. Cuando se dejaba caer la garra sobre un barco enemigo el brazo se movería para arriba, levantando el barco fuera del agua y hundiéndolo. Ha habido experimentos modernos para provar la garra, se construyo una version real del arma y se vio que funcionaba perfectamente. | |
== Principio de Arquímedes == | == Principio de Arquímedes == | ||
| Line 32: | Line 49: | ||
! fórmula | ! fórmula | ||
|- | |- | ||
| − | |E = | + | | |
| + | E= mg = pfgV | ||
|} | |} | ||
| − | |||
| − | |||
o bien | o bien | ||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 46: | Line 60: | ||
|- | |- | ||
| | | | ||
| − | + | E= mg = -pfgV | |
|} | |} | ||
| Line 59: | Line 73: | ||
=== Historia del Principio de Arquímedes === | === Historia del Principio de Arquímedes === | ||
| − | + | ||
[[File:Arquimedes Baño.jpg|200px|thumbnail|left|Arquímedes en el baño]] | [[File:Arquimedes Baño.jpg|200px|thumbnail|left|Arquímedes en el baño]] | ||
Según se cree, Arquímedes fue llamado por él el rey Herón de Siracusa, donde Arquímedes vivió en el siglo III A.C., para dilucidar el siguiente problema. Se cuenta que el rey Herón de Siracusa le había entregado a un platero una cierta cantidad de oro para con ella le hiciera una corona. Cuando estuvo terminada, se decía que el platero había sustituido una parte del oro por una cantidad equivalente de plata, devaluando con ello la corona y engañando, pues, al rey. | Según se cree, Arquímedes fue llamado por él el rey Herón de Siracusa, donde Arquímedes vivió en el siglo III A.C., para dilucidar el siguiente problema. Se cuenta que el rey Herón de Siracusa le había entregado a un platero una cierta cantidad de oro para con ella le hiciera una corona. Cuando estuvo terminada, se decía que el platero había sustituido una parte del oro por una cantidad equivalente de plata, devaluando con ello la corona y engañando, pues, al rey. | ||
| Line 68: | Line 82: | ||
Se dice que mientras se disponía a bañarse en una tina, en la que por error había puesto demasiada agua, al sumergirse en ella, parte del agua se derramó. Arquímedes se dio cuenta de que este hecho podía ayudarle a resolver el enigma planteado por Herón y fue tal su regocijo que, desnudo, salió corriendo de la tina gritando "¡Eureka, eureka!" (que significa "¡Lo encontré, lo encontré!"). | Se dice que mientras se disponía a bañarse en una tina, en la que por error había puesto demasiada agua, al sumergirse en ella, parte del agua se derramó. Arquímedes se dio cuenta de que este hecho podía ayudarle a resolver el enigma planteado por Herón y fue tal su regocijo que, desnudo, salió corriendo de la tina gritando "¡Eureka, eureka!" (que significa "¡Lo encontré, lo encontré!"). | ||
| − | + | ||
| + | |||
| + | [[File:Demostracion principio de arquímedes.png|thumbnail|Demostración del principio de arquímedes]] | ||
=== Demostración física === | === Demostración física === | ||
| − | + | [[File:Demostracion principio de arquímedes.png|thumbnail|Demostración del principio de arquímedes]] | |
| + | |||
| + | |||
| + | Cualquier cuerpo parcial o totalmente sumergido en un fluido sufre una fuerza vertical hacia arriba, llamada empuje, que es igual al peso del fluido que desaloja. | ||
| + | Imagina un cuerpo, por ejemplo, la corona de Arquímedes. Ahora imagina que el mismo cuerpo, con la forma exacta de la corona metálica estuviera hecho de agua –pues ése era el fluido en el caso de la historia– en vez de hecho de metal. ¿Cuánto pesaría esa “corona de agua”? Ése es el valor de la fuerza hacia arriba –el empuje– que sufre la corona metálica. | ||
| + | |||
| + | Un ejemplo es el de la pelota y la piscina. Estás tranquilamente en el agua, con una pelota junto a ti, e intentas meter la pelota bajo el agua, pero te cuesta muchísimo. ¿Cómo puede ser tan difícil hundir la pelota diez centímetros? | ||
| + | Porque, en tu cabeza, estás haciendo una cosa: hundir la pelota. | ||
| + | Pero, en la realidad, estás haciendo dos cosas, una muy fácil y otra no tanto: bajar la pelota y subir el agua. | ||
== Agradecimientos == | == Agradecimientos == | ||
| + | |||
| + | Muchas gracias a la señorita Irene Ariza, que con sus conocimientos hemos podido llevar a cabo este trabajo. Sin ella no habríamos hecho nada de esto. | ||
| + | |||
| + | Gracias a las páginas web que nos han servido como fuente de información, y que nos han servido para informarnos sobre todo. | ||
| + | |||
| + | Muchas gracias a todo el equipo, gracias a todos hemos conseguido terminar nuestra exposición. | ||
| + | |||
| + | Espero que les haya servido de ayuda. | ||
| + | |||
== Bibliografía == | == Bibliografía == | ||
| − | |||
| − | http://hidrostaticafisica2.blogspot.com.es/p/principio-de-arquimides.html | + | Alfredo Loayza y Tere Ledezma (abril de 2012). Principio de Arquímedes. ''Hidrostática''. Consultado el 12 marzo de 2014. En: http://hidrostaticafisica2.blogspot.com.es/p/principio-de-arquimides.html |
| + | |||
| + | Elbesodenarciso (2010, mayo 30). Arquímedes - Inventos y Descubrimientos. ''Taringa! inteligencia colectiva''. Consultado el 12 de marzo del 2014. En: http://www.taringa.net/posts/ciencia-educacion/5645290/Arquimedes---Inventos-y-Descubrimientos.html | ||
| + | |||
| + | Principio de Arquímedes de Siracusa. ''Wikipedia: La enciclopedia libre.'' Consultado el 26 de marzo de 2014. | ||
| + | En: http://es.wikipedia.org/wiki/Principio_de_Arqu%C3%ADmedes. | ||
| + | |||
| + | Arquímedes.(2014, marzo 3). ''Wikipedia: La enciclopedia libre.'' Consultado el 12 de marzo de 2014. | ||
| + | En: http://es.wikipedia.org/wiki/Arquímedes es.wikipedia.org/wiki/Arquímedes. | ||
| + | |||
| + | Miguel Ruiza y otros. Arquímedes. ''Biografías y vidas''. Consultado el 26 de noviembre de 2014. En: http://www.biografiasyvidas.com/biografia/a/arquimedes.htm | ||
| + | |||
| + | Arquímedes. (2014, marzo 17). ''Wikipedia: La enciclopedia libre.'' Consultado el día 26 mar 2014. | ||
| + | En: http://es.wikipedia.org/wiki/Arqu%C3%ADmedes | ||
| − | |||
| − | |||
| − | [[Category: Física | + | [[Category: Física]] |
[[Category: N15]] | [[Category: N15]] | ||
Latest revision as of 08:18, 26 April 2017
Contents |
Introducción
En este vídeo vamos a ver el Episodio 02 de Erase una vez los Inventores. En este vídeo no solo nos muestran los inventos de Arquímedes, sino también de muchos otros antiguos que descubrieron muchas cosas.
En este trabajo os vamos a hablar sobre Arquímedes de Siracusa y sus grandes teorías, y para ello, tenemos una breve introducción antes de adentrarnos en su biografía. Arquímedes fue un físico, ingeniero, inventor, astrónomo y matemático griego. Aunque se conocen pocos detalles de su vida, es considerado uno de los científicos más importantes de la antigüedad clásica. Entre sus avances en física se encuentran sus fundamentos en hidrostática, estática y la explicación del principio de la palanca. Es reconocido por haber diseñado innovadoras máquinas, incluyendo armas de asedio y el tornillo de Arquímedes utilizado para elevar agua, la polea compuesta, el torno y la rueda dentada. Experimentos modernos han probado las afirmaciones de que Arquímedes llegó a diseñar máquinas de guerra basadas en palancas, catapultas y un sistema de espejos con el que logró incendiar las naves romanas.
Se considera que Arquímedes fue uno de los matemáticos más grandes de la antigüedad y uno de los más importantes de la historia. Usó el método exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número Pi. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy largos. También debemos añadir que fue este ámbito el que más desarrolló ya que ante todo él se consideraba un verdadero geómetra colaborando en el desarrollo que se daría casi 2000 años más tarde del cálculo integral.
Las relativamente pocas copias de trabajos escritos de Arquímedes que sobrevivieron a través de la Edad Media fueron una importante fuente de ideas durante el Renacimiento, mientras que el descubrimiento en 1906 de trabajos desconocidos de Arquímedes en el Palimpsesto de Arquímedes ha ayudado a comprender cómo obtuvo sus resultados matemáticos.
Biografía
Nació en Siracusa en el 287 a.C y murió en el 212 a.C. Matemático griego. Hijo de un astrónomo, Arquímedes estudió en Alejandría, donde tuvo como maestro a Conón de Samos y entró en contacto con Eratóstenes. Regresó luego a Siracusa, donde se dedicó al trabajo científico.
Arquímedes: Gran matemático e ingeniero, a quien Plutarco atribuyó una «inteligencia sobrehumana. La más divulgada la relata Vitruvio y se refiere al método que utilizó para comprobar si existió fraude en la confección de una corona de oro encargada por Hierón II, tirano de Siracusa y protector de Arquímedes. Hallándose en un establecimiento de baños, advirtió que el agua desbordaba de la bañera a medida que se iba introduciendo en ella; esta observación le inspiró la idea que le permitió resolver la cuestión que le planteó el tirano. Se cuenta que, impulsado por la alegría, corrió desnudo por las calles de Siracusa hacia su casa gritando «Eureka! Eureka!».
La idea de Arquímedes está reflejada en su obra Sobre los cuerpos flotantes, corresponde al famoso principio que lleva su nombre y, como allí se explica, haciendo uso de él es posible calcular la ley de una aleación, lo cual le permitió descubrir que el orfebre había cometido fraude.
Otra anécdota famosa, recogida por Plutarco, entre otros, Arquímedes aseguró al tirano que," si le daban un punto de apoyo, conseguiría mover la Tierra"; se cree que, exhortado por el rey a que pusiera en práctica su aseveración, logró sin esfuerzo, mediante un complicado sistema de poleas, poner en movimiento un navío de tres mástiles con su carga.
Son célebres los ingenios bélicos, que permitieron a Siracusa resistir tres años el asedio romano, antes de caer en manos de las tropas de Marcelo; también se cuenta que, contraviniendo órdenes expresas del general romano, un soldado mató a Arquímedes por resistirse a abandonar la resolución de un problema matemático en el que estaba trabajando.
La pasión de Arquímedes por el conocimiento , que le causó la muerte, fue también la que, en vida, soliera entretenerse trazando dibujos geométricos en las cenizas del hogar o incluso, al ungirse, en los aceites que cubrían su piel. Esta imagen contrasta con la del inventor de máquinas de guerra del que hablan Polibio y Tito Livio; pero, como señala Plutarco, su interés por esa maquinaria estribó únicamente en el hecho de que planteó su diseño como mero entretenimiento intelectual.
El esfuerzo de Arquímedes por convertir la estática en un cuerpo doctrinal riguroso es comparable al realizado por Euclides con el mismo propósito respecto a la geometría; esfuerzo que se refleja de modo especial en dos de sus libros: en los Equilibrios planos fundamentó la ley de la palanca, deduciéndola a partir de un número reducido de postulados, y determinó el centro de gravedad de paralelogramos, triángulos, trapecios, y el de un segmento de parábola. En la obra Sobre la esfera y el cilindro utilizó el método denominado de exhaustión, precedente del cálculo integral, para determinar la superficie de una esfera y para establecer la relación entre una esfera y el cilindro circunscrito en ella. Este último resultado pasó por ser su teorema favorito, que por expreso deseo suyo se grabó sobre su tumba, hecho gracias al cual Cicerón pudo recuperar la figura de Arquímedes cuando ésta había sido ya olvidada.
Descubrimientos
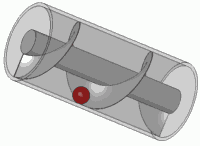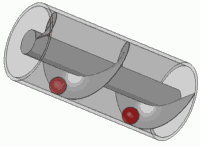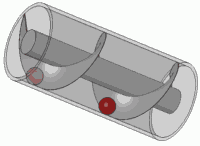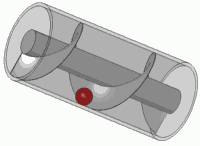
Uno de sus grandes inventos fue el tornillo de Arquímides que consistía en una máquina que era era un mecanismo con una hoja con forma de tornillo dentro de un cilindro. Se hacía girar por medio de una manivela, y podía utilizarse para transportar agua a niveles mas altos.
Principio de Arquímedes
El principio de Arquímedes es un principio físico que afirma que: «Un cuerpo total o parcialmente sumergido en un fluido en reposo, recibe un empuje de abajo hacia arriba igual al peso del volumen del fluido que desaloja». Esta fuerza recibe el nombre de empuje hidrostático o de Arquímedes, y se mide en newtons (en el Sistema Internacional de Unidades). El principio de Arquímedes se formula así:
| fórmula |
|---|
|
E= mg = pfgV |
o bien
| fórmula |
|---|
|
E= mg = -pfgV |
Donde E es el empuje , ρf es la densidad del fluido, V el «volumen de fluido desplazado» por algún cuerpo sumergido parcial o totalmente en el mismo, g la aceleración de la gravedad y m la masa, de este modo, el empuje depende de la densidad del fluido, del volumen del cuerpo y de la gravedad existente en ese lugar. El empuje (en condiciones normales y descrito de modo simplificado ) actúa verticalmente hacia arriba y está aplicado en el centro de gravedad del fluido desalojado por el cuerpo; este punto recibe el nombre de centro de carena.
Principio de Arquímedes de Siracusa
Historia del Principio de Arquímedes
Según se cree, Arquímedes fue llamado por él el rey Herón de Siracusa, donde Arquímedes vivió en el siglo III A.C., para dilucidar el siguiente problema. Se cuenta que el rey Herón de Siracusa le había entregado a un platero una cierta cantidad de oro para con ella le hiciera una corona. Cuando estuvo terminada, se decía que el platero había sustituido una parte del oro por una cantidad equivalente de plata, devaluando con ello la corona y engañando, pues, al rey.
El rey encargó a Arquímedes que descubriera si había sido engañado. El problema que Arquímedes debía resolver era determinar si el joyero había sustraído parte del oro o no, pero no podía romper la corona para averiguarlo. Arquímedes pensó arduamente cómo resolver el problema, sin poder encontrar una solución.
Se dice que mientras se disponía a bañarse en una tina, en la que por error había puesto demasiada agua, al sumergirse en ella, parte del agua se derramó. Arquímedes se dio cuenta de que este hecho podía ayudarle a resolver el enigma planteado por Herón y fue tal su regocijo que, desnudo, salió corriendo de la tina gritando "¡Eureka, eureka!" (que significa "¡Lo encontré, lo encontré!").
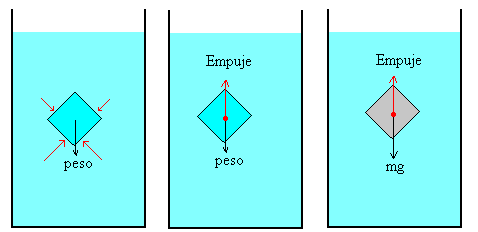
Demostración física
Cualquier cuerpo parcial o totalmente sumergido en un fluido sufre una fuerza vertical hacia arriba, llamada empuje, que es igual al peso del fluido que desaloja.
Imagina un cuerpo, por ejemplo, la corona de Arquímedes. Ahora imagina que el mismo cuerpo, con la forma exacta de la corona metálica estuviera hecho de agua –pues ése era el fluido en el caso de la historia– en vez de hecho de metal. ¿Cuánto pesaría esa “corona de agua”? Ése es el valor de la fuerza hacia arriba –el empuje– que sufre la corona metálica.
Un ejemplo es el de la pelota y la piscina. Estás tranquilamente en el agua, con una pelota junto a ti, e intentas meter la pelota bajo el agua, pero te cuesta muchísimo. ¿Cómo puede ser tan difícil hundir la pelota diez centímetros? Porque, en tu cabeza, estás haciendo una cosa: hundir la pelota. Pero, en la realidad, estás haciendo dos cosas, una muy fácil y otra no tanto: bajar la pelota y subir el agua.
Agradecimientos
Muchas gracias a la señorita Irene Ariza, que con sus conocimientos hemos podido llevar a cabo este trabajo. Sin ella no habríamos hecho nada de esto.
Gracias a las páginas web que nos han servido como fuente de información, y que nos han servido para informarnos sobre todo.
Muchas gracias a todo el equipo, gracias a todos hemos conseguido terminar nuestra exposición.
Espero que les haya servido de ayuda.
Bibliografía
Alfredo Loayza y Tere Ledezma (abril de 2012). Principio de Arquímedes. Hidrostática. Consultado el 12 marzo de 2014. En: http://hidrostaticafisica2.blogspot.com.es/p/principio-de-arquimides.html
Elbesodenarciso (2010, mayo 30). Arquímedes - Inventos y Descubrimientos. Taringa! inteligencia colectiva. Consultado el 12 de marzo del 2014. En: http://www.taringa.net/posts/ciencia-educacion/5645290/Arquimedes---Inventos-y-Descubrimientos.html
Principio de Arquímedes de Siracusa. Wikipedia: La enciclopedia libre. Consultado el 26 de marzo de 2014. En: http://es.wikipedia.org/wiki/Principio_de_Arqu%C3%ADmedes.
Arquímedes.(2014, marzo 3). Wikipedia: La enciclopedia libre. Consultado el 12 de marzo de 2014. En: http://es.wikipedia.org/wiki/Arquímedes es.wikipedia.org/wiki/Arquímedes.
Miguel Ruiza y otros. Arquímedes. Biografías y vidas. Consultado el 26 de noviembre de 2014. En: http://www.biografiasyvidas.com/biografia/a/arquimedes.htm
Arquímedes. (2014, marzo 17). Wikipedia: La enciclopedia libre. Consultado el día 26 mar 2014. En: http://es.wikipedia.org/wiki/Arqu%C3%ADmedes