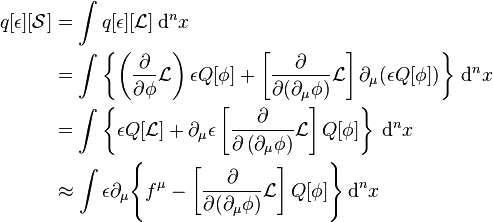Investigadores.15B.EmmyNoether.2018

BIOGRAFÍA:

Emmy Noether fue una importante matemática, que se hizo un lugar en la comunidad científica de principios del sXX, cuando las mujeres ni siquiera tenían derecho a acceder a los estudios universitarios. A pesar de haber elaborado teorías determinantes para las matemáticas, tuvo que luchar durante toda su vida para estar en el lugar que se merecía. Amalie Emmy Noether nació el 23 de marzo de 1882 en la ciudad de Erlange, Bavaria, Alemania. Pertenecía a una familia judía. Su madre, Ida Kauffman, era una mujer de la burguesía acomodada de Colonia y su padre, Max Noether, era profesor de matemáticas en la Universidad de Erlangen. Emmy Noether era la mayor de cuatro hermanos y pertenecía a una familia de matemáticos de varias generaciones. Emmy inició sus en 1889 en la escuela de su ciudad natal, donde permaneció hasta 1897. Tres años después aprobó con buena nota el examen para ejercer como profesora de idiomas. Aunque en aquella época el trabajo de maestra era uno de los pocos a los que una mujer podía aspirar, no era la vocación de Emmy. Durante los primeros años del s.XX, Emmy comenzó a asistir a clases de la universidad de manera extraoficial, aprovechando que su padre era el que las impartía. Poco después accedía a la Universidad de Gotinga (también de manera extraoficial), donde decidió especializar sus estudios en las matemáticas. En 1907 presentó su tesis doctoral Sobre la construcción de los sistemas formales de las formas ternaria cuadrática.

A lo largo de siete años se dedicó a trabajar en el Instituto de Matemáticas de Erlangen, normalmente sustituyendo a su padre y sin recibir un sueldo, por ser mujer. Además trabajó con los científicos principales del momento, redactó importantes teorías y redactó sus estudios de álgebra.

En 1915 volvió a Gotinga, a impartir clases, pero también como ayudante de otros profesores y recibiendo además el desprecio de alumnos y académicos que no veían bien la presencia de una mujer en un templo del saber.

En 1918 formuló el teorema que recibiría su nombre, debido a la gran importancia que supuso para la física moderna y que algunos científicos pusieron a la misma altura que el Teorema de Pitágoras. Posteriormente viajó a Rusia donde trabajó con científicos rusos en la Universidad Estatal de Moscú. En 1932 recibió un premio por su dedicación y gran contribución a las ciencias matemáticas. Esto le supuso ganar un dinero que le fue de gran ayuda, ya que hasta entonces había vivido mantenida por su familia. Aquel mismo año viajó a Zúrich donde participó como conferenciante en el Congreso Internacional de Matemáticos.

Con la llegada del nazismo, que supuso la expulsión de los judíos de todos los lugares públicos (incluidas las universidades), Emmy aceptó una oferta de una universidad de Pensilvania, Estados Unidos. Aquí, aunque recibió algún desprecio, vivió tranquila y feliz.

Hasta que en 1935 le diagnosticaron un tumor pélvico y un quiste ovárico que terminaron con su vida el 14 de abril de aquel mismo año. Sus cenizas fueron depositadas en la Biblioteca de la M.Carey Thomas Library de Brun Mawr. Su legado científico fue desde entonces reconocido en todo el mundo.

Teorías:

Muchos de sus estudios supusieron un punto de partida para un gran número de líneas de investigación, incluso en campos muy alejados al suyo, como la topología algebraica. Sin embargo, es principalmente conocida por formular el bautizado, en su honor, como Teorema de Noether. Este teorema tiene un gran número de aplicaciones prácticas en el campo de la física y, además, explica por qué existen leyes de conservación y magnitudes físicas que no cambian con el tiempo dentro de un sistema físico. - Emmy Noether fue una matemática famosa por sus aportaciones de los campos de la física teórica y álgebra y, por sus teorías: Gran parte del trabajo de Noether en la primera época de su carrera estaba asociado con la teoría de las invariantes algebraicas, principalmente la teoría de las matemáticas algebraicas. La teoría de los invariantes trata de las expresiones que permanecen constantes (invariantes) bajo grupos de transformaciones. Como ejemplo cotidiano, si una vara de medir rígida se somete a rotación, las coordenadas (x, y, z) de sus extremos cambian, pero su longitud dada las fórmulas.

Sus teorías revolucionaron el mundo matemático dejando a un lado los complejos sobre las mujeres.

¿Qué no sabías de Emmy Noether?

A lo largo de siete años se dedicó a trabajar en el Instituto de Matemáticas de Erlangen, normalmente sustituyendo a su padre y sin recibir un sueldo, por ser mujer. Además trabajó con los científicos principales del momento, redactó importantes teorías y redactó sus estudios de álgebra. En 1915 volvió a Gotinga, a impartir clases, pero también como ayudante de otros profesores y recibiendo además el desprecio de alumnos y académicos que no veían bien la presencia de una mujer en un templo del saber.Con la llegada del nazismo, que supuso la expulsión de los judíos de todos los lugares públicos (incluidas las universidades), Emmy aceptó una oferta de una universidad de Pensilvania, Estados Unidos. Aquí, aunque recibió algún desprecio, vivió tranquila y feliz.Posteriormente viajó a Rusia donde trabajó con científicos rusos en la Universidad Estatal de Moscú. En 1932 recibió un premio por su dedicación y gran contribución a las ciencias matemáticas. Esto le supuso ganar un dinero que le fue de gran ayuda, ya que hasta entonces había vivido mantenida por su familia. Aquel mismo año viajó a Zúrich donde participó como conferenciante en el Congreso Internacional de Matemáticos. En 1935 le diagnosticaron un tumor pélvico y un quiste ovárico que terminaron con su vida el 14 de abril de aquel mismo año. Sus cenizas fueron depositadas en la Biblioteca de la M.Carey Thomas Library de Brun Mawr. Su legado científico fue desde entonces reconocido en todo el mundo.