Resultante de un sistema de fuerzas. N15
Definición de una resultante de un sistema de fuerzas
La resultante es una fuerza que por sí sola producirá el mismo efecto que todo el sistema de fuerzas.
Si actúan varias a la vez sobre un cuerpo se han de aplicar, para su composición, las reglas de suma de vectores para hallar la resultante total que actúa sobre el cuerpo.
Por ejemplo,si dos caballos tiran de un carro en la misma dirección, uno con una fuerza de 150 kilogramos fuerza y el otro con una fuerza de 120 kilogramos fuerza, la fuerza resultante sería de 270 kilogramos fuerza. Puedes pensar que podríamos reemplazar los dos caballos por un buey que haga esa fuerza y obtendríamos el mismo resultado.
Ahora piensa que los pongamos a tirar a los mismos caballos en sentido opuesto, en ese caso la resultante será 30 kilogramos fuerza en dirección de caballo más fuerte.
Casos de fuerzas
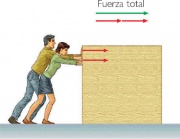
-Fuerzas con misma dirección y sentido: Si las fuerzas tienen la misma dirección se suman sus módulos (o se restan si su sentido es opuesto). La suma resultante representa el efecto combinado de todas las fuerzas y tiene su misma dirección.
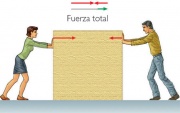
-Fuerzas con misma dirección pero sentido contrario: Si se aplican dos fuerzas concurrentes a un cuerpo con la misma dirección, aunque distinto sentido, pueden ser sustituidas por una única fuerza equivalente con la misma dirección y sentido que la mayor de las anteriores, aunque el modulo de esta nueva fuerza, sera´igual al valor absoluto de la resta de los módulos de las dos fuerzas
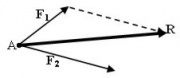
-Dos fuerzas con distinta dirección: en éste caso se aplica el Teorema de Varignon.
-Teorema de Varignon: el Teorema de Varignon es un teorema descubierto por primera vez por el matemático neerlandés Simon Stevin a principios del siglo XVII, pero que debe su actual forma al matemático francés Pierre Varignon (1654-1722), quien lo enunció en 1687 en su tratado Nouvelle mécanicque, como resultado de un estudio geométrico en el que, en contra de la opinión de los matemáticos franceses de su época, decidió trasladar las ideas expuestas por Newton a la notación y al enfoque que sobre el análisis sostenía Leibniz.
Bibliografía
Información sobre las fuerzas y como se forman
maszrb (3 de abril de 2014). Suma de fuerzas concurrentes. Fuerza resultante. Consultado el 7 de mayo de 2014. En: http://www.buenastareas.com/ensayos/Fuerza-Resultante/167483.html
Fisicalab (sin fecha). Suma de Fuerzas Concurrentes. Físicalab.com. Consultado el 7 de mayo de 2014. En: http://www.fisicalab.com/apartado/suma-fuerzas-concurrentes/intermedio
Profesor en línea (sin fecha). Sistemas de Fuerzas. Profesor en línea. Consultado el 7 de mayo de 2014. En: http://www.profesorenlinea.cl/fisica/Fuerzas_sistemas.html
Imágenes
Profesor en línea (sin fecha). Sistemas de Fuerzas. Profesor en línea. Consultado el 7 de mayo de 2014. En: http://www.profesorenlinea.cl/fisica/Fuerzas_sistemas.html